Fuzzy Control of Active Vehicle Suspensions for Enhanced Safety in Goods Transport
Abstract:
Suspension systems play a critical role in ensuring the safety, comfort, and stability of vehicles during the transportation of both passengers and goods. Among various suspension technologies, active or electronic suspensions have emerged as the most advanced due to their ability to dynamically adjust damping characteristics, thereby optimizing vehicle performance. This is typically achieved by modulating the pressure or flow of air or oil within the damper, or by altering its physical properties. To facilitate such dynamic adjustments, an effective control system is essential. Soft computing techniques, such as fuzzy logic controllers, are increasingly employed for their robustness and adaptability in providing the required control forces. In this study, the active suspension system was controlled via a fuzzy logic controller, with a piezoelectric actuator employed to generate the control force. A comparative analysis was conducted with traditional control methods, including the proportional-integral-derivative (PID) controller, to evaluate the performance of the fuzzy logic approach. Simulation results demonstrated that both control strategies were capable of achieving stable and smooth suspension behavior. However, fuzzy control was found to respond more quickly to dynamic changes, while the PID controller exhibited superior performance during the initial stages of vibration, offering enhanced safety during the commencement of transport. These findings underscore the potential of fuzzy logic control in optimizing the active suspension systems for improved vehicle dynamics and the safe transport of sensitive goods.1. Introduction
A suspension is a vital part for a vehicle's proper and smooth functioning. The kinematics and the geometry of a suspension system are among the most complex concepts in the automotive field. The suspension is the mechanism that keeps the wheels in contact with the road when the car is turning, accelerating or braking. It consists of shock absorbers, springs (as many as the wheels) and metal rods, which control the movement of the wheels through mechanical joints. The suspension determines the overall handling and comfort of the car. There are many types of suspensions, but they all have three main functions, namely, keeping the wheels as vertical as possible, regardless of the movement of the car, absorbing road abnormalities and ensuring the grip on the road, i.e., the stability and road behavior of the vehicle.
The most advanced suspension systems are the so-called active or electronic suspensions, where the damping of shock absorbers can be changed, modifying the dynamic characteristics and thus, the quality of the car’s rolling. This is achieved by changing the pressure or flow of air or oil in the shock absorber, or the properties of the fluid (cf. magnetorheological dampers). Some such suspensions even have the ability to change the height of the vehicle. All these features are controlled by a computer through a control system, which collects information from sensors about the quality of the road, the speed or acceleration of the vehicle, the steering wheel angle and the rotation speed, the accelerator pedal pressure, and the engine speed or pressure on the brake pedal, and, subsequently, configures the suspension.
An effective control of the suspension is important for the safety of the vehicle and the comfort of the passengers. For this reason, several methods have been proposed in the current literature to control the vibrations caused by the roadway in the suspension. Among others, fuzzy control [1], [2], [3], [4], [5], proportional-integral (PI) control [6], neural networks [7] and hybrid techniques [8], [9], [10] have been considered. For example, Phu and Choi [11] proposed an adaptive fuzzy-PID controller for the vibration control of a vehicle’s seat suspension. Moaaz and Ghazaly [12] compared fuzzy control with PID control for active suspensions in the frequency domain. If necessary, the fuzzy controller can be fine-tuned using global optimization methods, as analytically described by Tairidis et al. [13]. Optimal design of active suspension controllers with respect to safety requirements for goods transport seems to be an open field for research.
In most studies, the problem-solving approach is usually seen as a model that includes an axis, a suspension and a wheel. This system receives stimuli which depend on the typical unevenness of the ground and the speed of the system, and the response to these disturbances is observed. Fuzzy control is a very powerful soft computing tool, which is used not only in modern active suspension systems but also in several other engineering applications, such as the vibration control of smart structures, as described by Tairidis et al. [14], the wind energy sector [15], and robotics [16], [17], [18]. Emam [19] used an automatic control system with a fuzzy logic controller in order to minimize vertical acceleration for better passenger comfort and determine the position of the damper to avoid collision with the limits of the suspension, thereby reducing wear. A similar concept was proposed in the present study as it has realistic approaches and is easy to apply in a real-life environment.
2. Materials and Methods
The design and modelling of an active suspension system of a vehicle constitutes an interesting automated control problem. In this study, a quarter-vehicle suspension model, i.e., one of the four wheels, was considered. As seen in Figure 1, this concept simplifies the problem to a two-degree-of-freedom spring-mass-damper dynamic problem.

The equations of motion of the problem are given by Newton's second law of motion in terms of generalized coordinates as:
where, $m_1$ is the mass of the quarter-vehicle; $m_2$ is the mass of the whole system of the wheel, including steering, suspension, and so on; $k_1$ is the spring constant of the suspension system; $k_2$ is the spring constant of the wheel; $b_1$ is the damping constant of the suspension system; $b_2$ is the damping constant of the wheel; $x_1$ is the deflection of the vehicle; $x_2$ is the deflection of the suspension system; the first and second derivatives of $x_1$ and $x_2$ are the respective velocities and accelerations; $u$ is the control actuator force; and $W$ is the disturbance from the road. In this study, the masses, spring constants and damping constants were selected as follows: $m_1=500 \mathrm{~kg}, m_2=200 \mathrm{~kg}$, $k_1=70500 \mathrm{~N} / \mathrm{m}, k_2=150000 \mathrm{~N} / \mathrm{m}, b_1=370 \mathrm{~N} \cdot \mathrm{~s} / \mathrm{m}$ and $b_2=8620 \mathrm{~N} \cdot \mathrm{~s} / \mathrm{m}$. The disturbance of the road is $W=-0.1 \mathrm{~m}$.
A Mamdani-type fuzzy controller was developed within the MATLAB environment using the Fuzzy Logic Toolbox. The inputs of the controller were the deflection, the velocity and the acceleration of the body, while the output of the control was the actuator force which is necessary for the control of the active suspension. The membership functions of the fuzzy variables are depicted in Figure 2. The range of the first and the second input variables, i.e., the deflection and the velocity, was [-1, 1], and five membership functions (categories), namely, negative medium (NM), negative small (NS), zero (ZE), positive small (PS) and Positive Medium (PM) were considered for both variables. For the third input, i.e., the acceleration of the body, the range was [-0.1, 0.1] and three membership functions were considered, namely, negative (N), ZE and positive (P). The output variable (actuator force) had a range of values in the interval [-5000, 5000] and nine membership functions were used, namely, negative very big (NV), negative big (NB), NM, NS, ZE, PS, PM, positive big (PB) and positive very big (PV).




The fuzzy rule base was written considering the movement and the control of a pendulum. The number of rules which are necessary for the decision-making unit of the fuzzy system was derived according to the number of the fuzzy input variables and its membership functions. In the controller proposed in this study, 50 if-then rules were used for the description of the fuzzy inference system. These verbal rules are given analytically in Table 1.
The graphic representation (surface) of the rules for the three inputs and the one output is depicted in pairs of inputs over the output, as shown in Figure 3.
| Rule | $\boldsymbol{X_1-X_2}$ | $\boldsymbol{V_1-V_2}$ | $\boldsymbol{A_1-A_2}$ | F | Rule | $\boldsymbol{X_1-X_2}$ | $\boldsymbol{V_1-V_2}$ | $\boldsymbol{A_1-A_2}$ | F |
| $\mathrm{R}_1$ | PM | PM | ZE | ZE | $\mathrm{R}_{26}$ | PM | PM | not ZE | NS |
| $\mathrm{R}_2$ | PS | PM | ZE | NS | $\mathrm{R}_{27}$ | PS | PM | not ZE | NM |
| $\mathrm{R}_3$ | ZE | PM | ZE | NM | $\mathrm{R}_{28}$ | ZE | PM | not ZE | NB |
| $\mathrm{R}_4$ | NS | PM | ZE | NM | $\mathrm{R}_{29}$ | NS | PM | not ZE | NB |
| $\mathrm{R}_5$ | NM | PM | ZE | NB | $\mathrm{R}_{30}$ | NM | PM | not ZE | NV |
| $\mathrm{R}_6$ | PM | PS | ZE | ZE | $\mathrm{R}_{31}$ | PM | PS | not ZE | NS |
| $\mathrm{R}_7$ | PS | PS | ZE | NS | $\mathrm{R}_{32}$ | PS | PS | not ZE | NM |
| $\mathrm{R}_8$ | ZE | PS | ZE | NS | $\mathrm{R}_{33}$ | ZE | PS | not ZE | NM |
| $\mathrm{R}_9$ | NS | PS | ZE | NM | $\mathrm{R}_{34}$ | NS | PS | not ZE | NB |
| $\mathrm{R}_{10}$ | NM | PS | ZE | NM | $\mathrm{R}_{35}$ | NM | PS | not ZE | NB |
| $\mathrm{R}_{11}$ | PM | ZE | ZE | PS | $\mathrm{R}_{36}$ | PM | ZE | not ZE | PM |
| $\mathrm{R}_{12}$ | PS | ZE | ZE | ZE | $\mathrm{R}_{37}$ | PS | ZE | not ZE | PS |
| $\mathrm{R}_{13}$ | ZE | ZE | ZE | ZE | $\mathrm{R}_{38}$ | ZE | ZE | not ZE | ZE |
| $\mathrm{R}_{14}$ | NS | ZE | ZE | ZE | $\mathrm{R}_{39}$ | NS | ZE | not ZE | NS |
| $\mathrm{R}_{15}$ | NM | ZE | ZE | NS | $\mathrm{R}_{40}$ | NM | ZE | not ZE | NM |
| $\mathrm{R}_{16}$ | PM | NS | ZE | PM | $\mathrm{R}_{41}$ | PM | NS | not ZE | PB |
| $\mathrm{R}_{17}$ | PS | NS | ZE | PM | $\mathrm{R}_{42}$ | PS | NS | not ZE | PB |
| $\mathrm{R}_{18}$ | ZE | NS | ZE | PS | $\mathrm{R}_{43}$ | ZE | NS | not ZE | PM |
| $\mathrm{R}_{19}$ | NS | NS | ZE | PS | $\mathrm{R}_{44}$ | NS | NS | not ZE | PM |
| $\mathrm{R}_{20}$ | NM | NS | ZE | ZE | $\mathrm{R}_{45}$ | NM | NS | not ZE | PS |
| $\mathrm{R}_{21}$ | PM | NM | ZE | PB | $\mathrm{R}_{46}$ | PM | NM | not ZE | PV |
| $\mathrm{R}_{22}$ | PS | NM | ZE | PM | $\mathrm{R}_{47}$ | PS | NM | not ZE | PB |
| $\mathrm{R}_{23}$ | ZE | NM | ZE | PM | $\mathrm{R}_{48}$ | ZE | NM | not ZE | PB |
| $\mathrm{R}_{24}$ | NS | NM | ZE | PS | $\mathrm{R}_{49}$ | NS | NM | not ZE | PM |
| $\mathrm{R}_{25}$ | NM | NM | ZE | ZE | $\mathrm{R}_{50}$ | NM | NM | not ZE | PS |



A PID controller was developed in order to check the efficiency of the control in comparison to a more classical control approach. In order to apply the PID controller to the system, it is necessary to calculate the transfer function of the plant (suspension model) and the disturbance (road abnormalities). Considering that all the initial conditions are zero, that is, the moment that the wheel of the vehicle receives a disturbance from the road, Eqs. (1) and (2) can be reformulated through Laplace transformation, yielding the transfer functions $G_1(s)$ and $G_2(s)$ with output $x_1-x_2$ and inputs $u$ and $W$, as follows:
If
Taking the inverse of matrix $A$, the following can be obtained by using its determinant $\Delta$ and multiplying the inputs $U(s)$ and $W(s)$ with $1 / \Delta$ :
When only the study of input $U(s)$ is needed, then $W(s)=0$ can be set. As a result, the transfer function $G_1(s)$ is given as:
When the study of the disturbance $W(s)$ is of interest, $U(s)=0$ can be set, obtaining the transfer function $G_2(s)$ as:
The transfer function of the PID controller $G_c(s)$ is given as:
where, $K_P, K_I$ and $K_D$ are the proportional, the integral and the derivative terms, respectively, of the PID controller.
The feedback control system with the respective transfer functions for each element (plant, controller and external disturbance) is shown in Figure 4.
The transfer function $F(s)$ of the disturbance can be calculated from the block diagram of Figure 4 as follows:
The three gains of the PID controller, i.e., the numerical values for the three terms, were selected with trial and error as $K_P=1200, K_I=500$, and $K_D=450$. Several methods, such as the Ziegler-Nichols method, or optimization procedures (e.g., a genetic algorithm) can also be used for the selection and/or fine-tuning of the values for the three terms of the PID controller if necessary.

3. Results
For the simulation of the active suspension, as described in Subsection 2.1, the Simulink package of MATLAB was used. More details about the Simulink modelling are provided in Appendix.
Table 2 shows the maximum and minimum diversion of the deflection, velocity and acceleration of the body from the equilibrium point for the passive system, i.e., the one without any control.
For the control of these vibrations, two different configurations were considered: one with a controller based on fuzzy logic, and one with a three-term (PID) controller, as shown in Subsections 3.1 and 3.2, respectively.
| Passive | Fuzzy | PID | ||||||
X1-X2 (m) | V1-V2 (m/s) | A1-A2 (m/s2) | X1-X2 (m) | V1-V2 (m/s) | A1-A2 (m/s2) | X1-X2 (m) | V1-V2 (m/s) | A1-A2 (m/s2) | |
Max | 4.96×10-2 | 1.003 | 37.18 | 3.42×10-2 | 0.907 | 33.64 | 0.98×10-2 | 0.056 | 1.47 |
Min | -5.03×10-2 | -0.675 | -19.32 | -3.94×10-2 | -0.973 | -19.66 | -0.79×10-2 | -0.498 | -1.42 |
In the first layout, the fuzzy controller which is analytically described in Subsection 2.2 was used. The simulation time was set to 5 seconds. The results for the deterioration of vibrations in terms of deflection, velocity and acceleration of both passive (without control) and active (with fuzzy control) systems are graphically presented in Figure 5, Figure 6, and Figure 7, respectively. The actuator control force obtained by the fuzzy controller is depicted in Figure 8.




The maximum and minimum diversion of the parameters of interest for the system with the fuzzy controller are given in Table 2. Moreover, as seen in Table 3, the vibrations in terms of deflection were suppressed by 26.35% after the application of control. Velocity was increased by 12.02%, due to the high values between 1 and 1.5 seconds, as seen in Figure 6, while acceleration was reduced by 5.66%.
Passive vs. Fuzzy | Passive vs. PID | ||||
$\boldsymbol{X_1-X_2(\%)}$ | $\boldsymbol{V_1-V_2(\%)}$ | $\boldsymbol{A_1-A_2(\%)}$ | $\boldsymbol{X_1-X_2(\%)}$ | $\boldsymbol{V_1-V_2(\%)}$ | $\boldsymbol{A_1-A_2(\%)}$ |
26.35 | -12.02 | 5.66 | 82.43 | 93.51 | 94.31 |
In the second setup, the PID controller, as described in Subsection 2.3, was applied to the active suspension model. The simulation time was again set to 5 seconds and the control results in terms of deflection, velocity and acceleration of both passive and PID controlled systems are presented in Figure 9, Figure 10, and Figure 11, respectively.



The maximum and minimum deflection, velocity and acceleration for the active suspension with the PID controller are shown in Table 2. The reduction percentage of vibrations in this case for the three studied variables is given in Table 3. The deflection was suppressed by 82.43% after the application of the PID controller to the system, and, at the same time, velocity and acceleration were also reduced by 93.51% and 94.31%, respectively.
4. Discussion
The passive system, i.e., the suspension model prior to the application of any control, presents significant vibrations. More specifically, the maximum width of these vibrations in terms of deflection, velocity and acceleration is $9.99 \times 10^{-2} \mathrm{~m}, 1.68 \mathrm{~m} / \mathrm{s}$, and $56.5 \mathrm{~m} / \mathrm{s}^2$, respectively.
From the numerical experiments of the first control configuration, i.e., the one with the fuzzy system, it showed that the vibrations in terms of deflection settled down right after 1.5 seconds with a maximum width of $7.36 \times$ $10^{-2} \mathrm{~m}$. The system was also damped in terms of velocity right after 2 seconds of time with a width of $1.88 \mathrm{~m} / \mathrm{s}$, while the acceleration settled down before 2 seconds after the external disturbance, presenting a vibration width which equals $53.3 \mathrm{~m} / \mathrm{s}^2$.
Correspondingly, in the case where the PID controller was used, it showed that the deflection did not settle down completely within the 5 seconds of simulation, but, instead, it followed the one of the passive system after 2.5 seconds. The maximum width in this case was $1.78 \times 10^{-2} \mathrm{~m}$, which is significantly lower than the corresponding value of the previous case. However, the damping was much slower. A similar behavior was seen also for the velocity of the system, with a maximum vibration width which equals $0.1 \mathrm{~m} / \mathrm{s}$. Finally, the acceleration in the case of the system with the PID controller was very smooth, even if it seemed not to settle down within the 5 seconds of the simulation. The width in this case was $2.89 \mathrm{~m} / \mathrm{s}^2$ which is an impressive performance.
5. Conclusions
In summary, it can be observed that the active suspension controlled by a fuzzy system damped the vibrations, which were caused by road abnormalities, significantly faster compared to the one equipped with a PID controller. More specifically, the fuzzy controller managed to reduce the vibrations in less than two seconds, while almost 5 seconds or more were required by the PID system for the same assignment. However, PID control seemed to work smoother, especially in the first one to two seconds, as the width of vibrations within this time frame was significantly smaller for all three variables of interest, namely, the deflection, the velocity and the acceleration. For this reason, a hybrid scheme based on the combination of fuzzy systems and PID control may provide better results and thus, it can be an object of further study. Moreover, this hybrid control scheme can be optimized using neural networks, genetic algorithms, or other nature-inspired optimization methods, if necessary. The requirements and the choice of the controller may depend on the need of transported goods or equipment.
Conceptualization, K.M., G.K.T. and G.E.S.; methodology, G.K.T.; software, G.K.T., K.M..; validation, G.K.T., K.M. and A.P.; formal analysis, G.K.T.; data curation, K.M., A.P.; writing—original draft preparation, G.K.T.; supervision, G.E.S. All authors have read and agreed to the published version of the manuscript.
The data used to support the research findings are available from the corresponding author upon request.
This research project would not have been possible without the excellent participation and cooperation of Dr. G. K. Tairidis, who passed away in February 2022. We also gratefully acknowledge the partial support from the Erasmus+ project titled "Transport of Dangerous Goods – Modernization of Curricula and Development of Trainings for Professionals in the Western Balkans HEIs (DGTRANS)” (Contract No.: 101082187-DGTRANS-ERASMUS-EDU-2022-CBHE).
The authors declare no conflict of interest.
The Simulink model diagrams which were developed for this study are presented below. The results are presented by means of the Scope blocks; however, if necessary, they can be extracted to MATLAB’s workspace using the Simout command. The model for the active suspension with fuzzy control is depicted in Figure A1. Two subsystems, one for the passive and one for the fuzzy system, were developed, as shown in Figures A2 and A3, respectively. The Simulink model for the PID-controlled suspension is depicted in Figure A4. The subsystem of this model is the one of the passive systems, as seen in Figure A3.
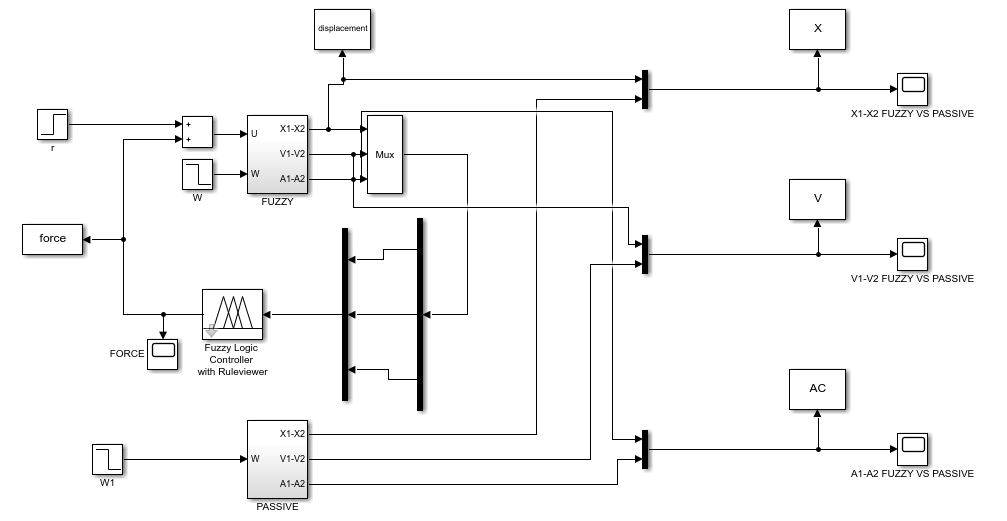
Figure A1. The Simulink model for the comparison between the passive and the fuzzy system

Figure A2. The Simulink model for the fuzzy subsystem
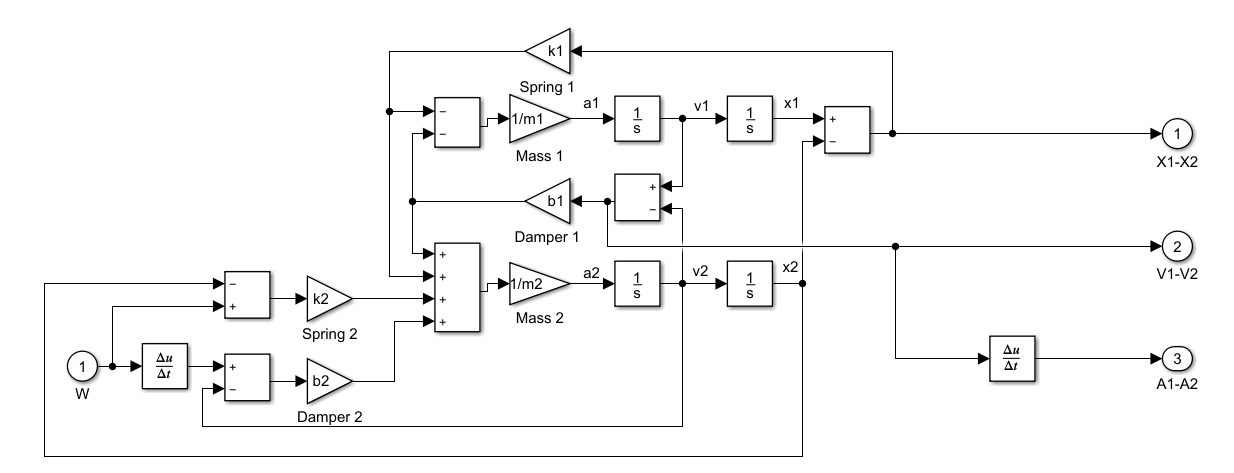
Figure A3. The Simulink model for the passive subsystem
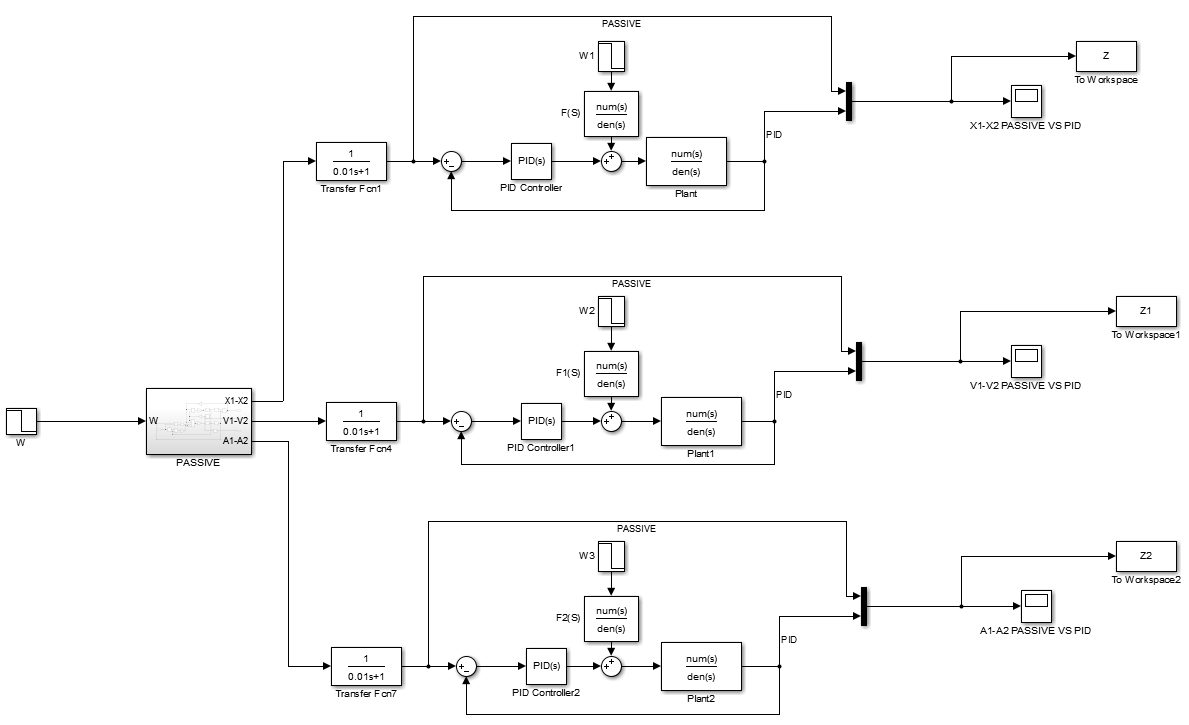
Figure A4. The Simulink model for the comparison between the passive and the PID system
