Built-in Premium Effects within Exotic FX Options

The focus of this paper is on premium-free options which are becoming very popular within the Forex (FX) industry as a risk management tool. Forex risk is being given more importance due to unexpected volatilities within the forex market, which left some corporations and industries, struggling due to foreign exchange losses. Such option strategies are not easy to understand and they are also not straight forward to value. Hence, making it very difficult for industries and academics to fully understand their risk, return and hidden costs. Through analysis conducted by the authors, readers would gain valuable information about the risk and return of such strategies based on a sample of seven years, over which hundreds of contracts were simulated using the Bloomberg terminal’s back-testing procedure.

The analysis was conducted on three major currency pairs. These were the EURUSD, Euro against the US Dollar, the EURGBP, Euro against the British Pound, and EURJPY, Euro against the Japanese Yen. The analysis was done using two different FX Option strategies-namely, the Window Forward Extra and the At-Expiry Forward Extra. The strategies are similar to each other with the main difference being that the Window Forward Extra uses an ‘American’ Knock-in Option – meaning that it is riskier in nature. The aim of using these two strategies was to analyse whether the extra risk had an extra effect on the outcome of these strategies when results were compared with those of the At-Expiry Forward Extra. The authors also analysed the outcome of the strategies should these be used for speculative purposes. The aim was to analyse two possibilities that the speculator would have. The first possibility is to take less risk and receive a lower or no upfront premium. The second possibility would be to increase the risk and in return receive a high up-front premium. The analysis was also conducted throughout the sever year period and results were compared.

According to the BIS report Triennial Central Bank Survey published in 2013, the daily global FX Turnover amounted to US\$5 Trillion. Furthermore the USD was the most traded currency with over 87% of trades was with the USD on one side. Intra-dealer trades also increased from US\$1.5 Trillion in 2010 to US\$2.2 Trillion in 2013.

Wystup (2006) noted that the first option recorded took place in 1728. This was a stock option which was offered by the Royal West-Indian and Guinea Company, which happened to be a monopolist when it came to trading within the Caribbean Islands and the African coast during that period. The options were on the purchase of the French Island of St. Croix which was valuable due to sugar plantings that were being planned to happen on the island. Furthermore, Wystup (2006) noted that the first future contract was recorded in ancient Greece. At that time, olives were purchased before they riped to ensure that enough olives were secured for the production of olive oil. This shows that even though the way we use options today has changed due to technological improvement, the foundations of this industry has been with us for a long time.

Exotic Options

The term exotic options came along due to the higher complexity such options have when compared to the simple ‘plain vanilla option’. A plain vanilla option may be defined as the purchase of a right to buy or sell a particular asset at a known price and a known future date. For this paper, the authors are more interested in the foreign exchange options. A plain vanilla FX option would give its holder the right to buy a particular currency and sell another at a known forex rate, notional amount at a predetermined date and time in the future.

Knock-ins and Knock-outs

The plain vanilla option may not be suitable for certain transactions within the FX industry. Hence, as technology improved, exotic options were being designed mostly to satisfy the growing need to design tailor-made structured products for large corporations. Knock-ins and Knock-outs are the most important as they are widely used in structured FX products. The authors used the knock-in option within this paper, however, they also felt the need to explain how the knock-outs work due to the fact that they may also be used together in certain products that have not been tested in this paper.

Hull (2006) defined these options as “barrier options” explaining that they “are options where the payoff depends on whether the underlying asset’s price reaches a certain level during a certain period of time”. He also noted that these are regularly traded over-the- counter (OTC) and “can be classified as either knock-out options or knock-in options” Furthermore, DeRosa (2011) identified a knock-in barrier option as “an option that does not come into existence unless the spot exchange rate breaches a specifiedin-strikelevel. The in-strike of the knock-in is located out-of-the-money. If the in-strike level (barrier level) trades, the knock-in permanently becomes a vanilla put or call. If the in-strike never trades, the knock-in will expire worthless at expiration, even if it is in-the-money”. In addition to this, a knock-out option was described by Bouzoubaa and Osseiran (2010) as “‘extinguishable’ options, which are path-dependent options that are terminated if a specified spot’s price reaches a specified trigger level at any time between inception and expiry”.

Constructing a Forward Extra

“A Forward Extra is constructed by combining two options: buying a plain vanilla option and selling a knock-in option. The structure is considered as a ‘zero-premium’ or ‘zero cost’ product within the OTC market. The reason behind this is that the holder of the product does not pay a premium upfront. This is possible since the product provider makes money by buying a cheaper vanilla and selling a more expensive knock-in option having the same strike and maturity but being a different option, that is, a call or a put” Caruana (2016)

How is the ‘zero-premium’ achieved?

As explained by Caruana (2016), there is an expectation that the market maker buy the vanilla call option at a premium and at the same time selling the knock-in put option at a premium.

Therefore, the holder of the product will sell the right to sell the underlying if the knock- in level (barrier level) is breached.making the holder obliged to buy the underlying at the strike rate. This will cancel out the premiums, since the premium paid for the call option is lower than the premium received for selling a put with a knock-in due to the risk involved.

For example,

Assume that the long USD call for 1 million USD notional at the strike of 1.3000 and the expiry being one year from now costs a premium of USD 10,000. On the other hand, selling a knock-in USD put option with a strike of 1.3000 and a knock-in level of 1.3500 having the same expiry and notional pays a premium of USD 15,000. Although for the client the product is offered at ‘zero-premium’, the broker or market maker made a profit of USD 5,000, being the ‘excess premium’ received over and above the cost of the long vanilla call option. The price sensitivity of the knock-in depends heavily on the implied volatility used in the pricing model of the market maker. It is ideal that one understands the dynamic of the knock-in instrument. The premium paid, or received, for, or from, a knock-in option would depend mostly on the barrier level and the type of barrier. As one expects, the standard option pricing factors, being the strike, spot level, time to maturity and implied volatility also play a crucial part on the premium received or paid for such a knock-in option. Caruana (2016)

The main differences between the Window Forward Extra and At-Expiry Forward Extra

The authors used two zero-premium strategies as noted above. There is one major difference between the two strategies which is related to the knock-in option built-in within the strategy itself. For the At-Expiry Forward Extra, the knock-in option is a European Option. This means that for the knock-in option to become ‘alive’, the barrier needs to be breached only at expiry time and date. Should the barrier be breached before, then such breach will be ignored. On the otherhand, when it comes to the Window Forward Extra, the built-in knock-in option is an ‘American Option’. This means that the barrier could be breached any time during a specified period of time. Hence, by nature, the Window Forward Extra is riskier as it has a larger probability tha the barrier level is breached which would result in a loss for the holder of the option strategy.

The possible outcomes of the At Expiry Forward Extra

The At Expiry Forward Extra has 3 possible outcomes. The first possible outcome is that the spot price at expiry is less valuable than the strike of the strategy. In that case, the holder of the strategy will have the right, not the obligation, to exercise the option at the strike price. This would result as a benefit for the holder of the strategy. The second possible outcome is that the spot price at expiry is more valuable than the strike price and is still less valuable than the barrier level. In such a scenario the holder of the option strategy would have no obligations but may wish to trade any amount in the spot market which would be more beneficial than the ‘worst case rate’ (hedge) of the strategy. In reality, this is the best case scenario for the holder of the option strategy as through this possibility the holder would get the best rate possible without having been fully exposed to the spot market. The third and final possible outcome of the strategy is that the spot price at expiry is more valuable than the barrier level. In this case, the barrier level would have been breached and so the holder of the strategy would have the obligation to execute at the strike rate which would be a more expensive rate than the spot price at expiry. This may be considered to be the worst case scenario of the strategy.

The possible outcomes of the Window Forward Extra

The Window Forward Extra has 3 possible outcomes. The first possible outcome is identical to that of the ‘at expiry forward extra’, that is, if the spot price is less valuable than the strike price of the option, then the holder of the option strategy would have the right, not the obligation, to transact at the strike price. The second possible outcome of the option strategy is, when the spot price is more valuable than the strike price but it was not as valuable or more valuable than the barrier level during the barrier level period. In such a scenario the holder of the option strategy would have no obligations but may wish to transact in the spot market which would be more beneficial. The final outcome would be if the spot price at expiry is more valuable than the strike price and the value of the spot has reached or exceeded the value of the barrier level during the barrier level period, then the holder of the strategy would have an obligation to transact using the strike price. Hence, one may note that the main difference is the reference of the ‘barrier level period’ within the American barrier. Such period is that particular period in which the barrier level would be ‘live’. Hence, should the barrier level be breached during this period, the knock-in would become alive which would in turn make the holder of the strategy buy at strike price.

The main aim of this paper is to analyse the effects of built-in premiums within zero- premium option strategies. The authors feel this is important for the industry because market makers and brokers would be able to take decisions on the level of ‘mark-up’ they would be making when quoting these strategies. On the other hand the client is unlikely to know the level of mark-up effectively being ‘paid’ since the value of these strategies depends on their time value and the implied volatility. To value these strategies the client would need to be knowledgable on their structure, have access to a valuation model such as bloomberg terminal, and have the time to structure and price it in an efficient manner. Hence, the authors assume that it is highly unlikely that this would take place.

Therefore, it is important to understand how the client would be effected by an increase of built-in premium. Furthermore, the authors also analysed the possibility of these strategies being used as a speculative tool, even though the main purpose is for hedging. Speculation can be done mostly by market makers or brokers which would have the possibility of either trading themselves at a low or zero built-in premium and receiving nothing upfront by the market maker, or increasing the risk of the strategy by adding built- in premium and hence receiving an upfront premium, which may be seen as a ‘guaranteed return’ before any market movement. The authors analysed both scenarios and carried out a backtesting over a period of 7 years.

This paper is based on a research conducted through two IT applications namely the Bloomberg Terminal and Matlab. These two mentioned strategies were designed and constructed using the OVML pricing model within the Bloomberg Terminal. This was done for the three currency pairs mentioned earlier in this paper. Hence, the analysis was done on six different scenarios, being, EURUSD – At Expiry Forward Extra, EURUSD – Window Forward Extra, EURGBP – At Expiry Forward Extra, EURGBP – Window Forward Extra, EURJPY – At Expiry Forward Extra, EURJPY – Window Forward Extra. For each scenario, a backtesting was carried out between 1st January 2007 up until December 2014.

The backtesting used the following assumptions:

a) The most important one is that the tenor of each strategy would be of 1 year. This was done on a monthly basis. Therefore, after each month another strategy for 1 year was done. Hence, following the first year of the analysis, there was an expiry every month for each scenario.

b) The second assumption is related to the level of the strike rate from the spot rate. This was decided to be fixed at 1% away from the spot when the pricing was done (back testing). Hence, the value of the strike will always be 1% less valuable than the spot rate when the pricing was done and when the option strategy starts. The barrier level was adjusted according to the built-in premium of the strategy and after the model takes in consideration the time value and implied volatility at the time that the strategy was starting.

Each scenario was split into a number of sub-scenarios, depending on the built-in premium being tested. These were 0%, 0.3%, 0.5%, 0.7% and 1%. One should note that for the EURJPY the 1% was not possible due to market limitations, hence, for the EURJPY, the maximum possible built-in premium after taking everything in consideration was at 0.7%. Hence, different combinations of backtests were performed using the bloomberg Terminal as follows: EURUSD – At Expiry Forward Extra, - 0% built-in premium; 0.3% built-in premium; 0.5% built-in premium; 0.7% built-in premium and 1% built-in premium. This was repeated for the Window Forward Extra strategy and also repeated for the EURGBP and EURJPY. For each expiry a notional amount of 1 million was also assumed. Results were exported to excel from the bloomberg terminal. After such data was exported to Excel, Matlab was coded in order to analyse such data. Results were then extracted back to excel for final analysis. Vide the sample code below:

close all

clear all

a = xlsread('dissertation data EURUSD.xls','AEFE 0 percent EURUSD');

strike_G = a(:,6);

barrier_i = a(:,8);

spot_n = a(:,13);

spotexpiry_s = a(:,18);

l = a(:,11);

forward= a(:,15);

profit=zeros(1,84);

x = zeros(84,10);

for i = 1:84

if spotexpiry_s(1+(3*i)) >= barrier_i(1+(3*i))

profit(i)= ((strike_G(1+(3*i)) - spotexpiry_s(1+(3*i)))*l(1+(3*i)));

elseif spotexpiry_s(1+(3*i)) < barrier_i(1+(3*i)) && spotexpiry_s(1+(3*i))>strike_G(1+(3*i))

profit(i) = (spotexpiry_s(1+(3*i))- forward(1+(3*i)))*l(1+(3*i));

elseif spotexpiry_s(1+(3*i))

profit(i)=(strike_G(1+(3*i)) - spotexpiry_s(1+(3*i)))*l(1+(3*i));

end

end

for i = 1:84 %same as above but for the 0.3% premium level

if spotexpiry_s_1(1+(3*i)) >= barrier_i_1(1+(3*i))

profit_1(i)= ((strike_G_1(1+(3*i)) - spotexpiry_s_1(1+(3*i)))*l_1(1+(3*i)));

elseif spotexpiry_s_1(1+(3*i)) < barrier_i_1(1+(3*i)) && spotexpiry_s_1(1+(3*i))>strike_G_1(1+(3*i))

profit_1(i) = (spotexpiry_s_1(1+(3*i))- (forward_1(1+(3*i))- forward_1(1+(3*i))* 0.003))*l_1(1+(3*i));

elseif spotexpiry_s_1(1+(3*i))

profit_1(i)=(strike_G_1(1+(3*i)) - spotexpiry_s_1(1+(3*i)))*l_1(1+(3*i));

end

end

The above code was repeated and adjusted for all currency pairs and built-in premium adjustments. The result from the above coding was exported to excel where the changes of built-in premium from one level to another is calculated. If the change is zero, then there is no effect in the built-in premium.

Such results were then tested for significance using a paired sample t-test. A 1-tail test was done since we can never expect to have a positive result when increasing the built-in premium. That is, the best case scenario would be that there is no negative effect nor positive effect. The hypothesis for such t-test is as follows:

HO: Mean returns vary marginally between the two strategies under test

HA: Mean returns vary significantly between the two strategies under test

Furthermore, the following combinations were tested for each currency pair and strategy. Please note that for the EURJPY pair number 4, 7, 9 and 10 were excluded due to market limitations as previously explained by the authors.

Total Profits or Losses of strategies

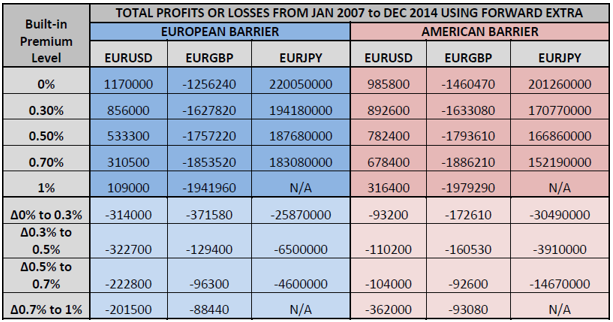
Table 2 below shows the profits or losses from the strategies under analysis for each level of built-in premium. This is also split between ‘european barrier’ and ‘american barrier’ being the at expiry forward extra and window forward extra respectively. Furthermore, table 2 shows the change between one level of premium to another. The below shows the totals for the whole period under consideration and does not capture the individual expiry results. Hence, as the readers can note, any increase of built-in premium resulted in a negative effect on the total outcome of each strategy.

Table 2

Built-in premium effects per expiry

Table 3

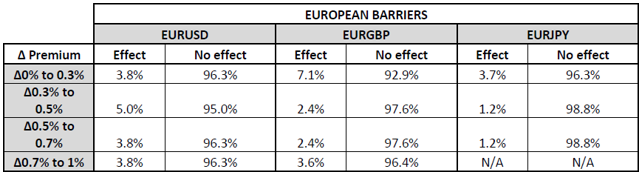
Table 4

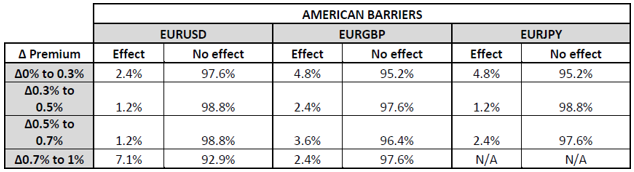
Tables 3 and 4 above show the level of effect of the respective change of built-in premium for european barrier and american barriers. An effect would mean that the change of built- in premium is non-zero. Hence, as one may note, for example, for european barriers using the EURUSD, when increasing the built-in premium from 0% to 0.3%, in 96.3% of the cases there was no effect, while in 3.8% of the cases there was an effect. For changes between 0.3% to 0.5%, an effect took place only in 5% of cases, so on and so forth. Hence, to summarise tables 3 and 4, in most cases, when analysing the effect per expiry, such effect is minimal.

Paired sample t-test on changes in outcome

As noted earlier in this paper, the authors tested the statistical significance of results using a one tail paired sample t-test. Should the tests result to be statistically significant, this would mean that there is a total statistically significant effect when increasing the built-in premium. Different combinations were tested as noted in table 1.

Table 5

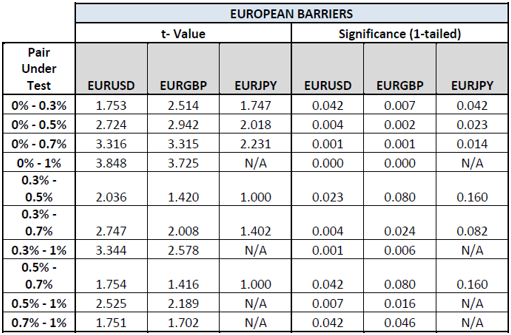
Table 5 above shows the t-values and statisitcal significance of tests conducted on the exotic options strategies using a european barrier. As can be noted in most cases the test is statistically significant at 95% confidence level. In some cases this is also significant at the 99% confidence level such as the EURUSD 0% to 1%, 0% to 0.7%, 0% to 0.5%, 0.3% to 0.7% etc.

Table 6

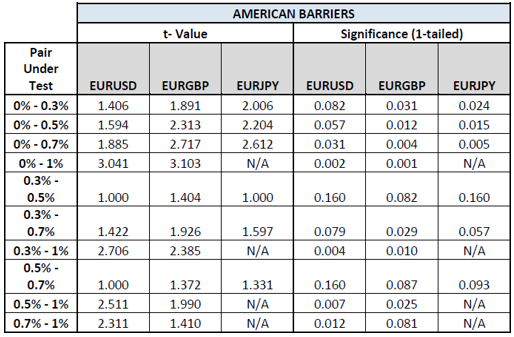
Table 6 shows the t-test results when using american barrier within the strategy. Similar results to those in Table 5 can be noticed. This shows that the increase in risk from using a riskier strategy does not have much effect.

Summary of statistical significance

Table 7

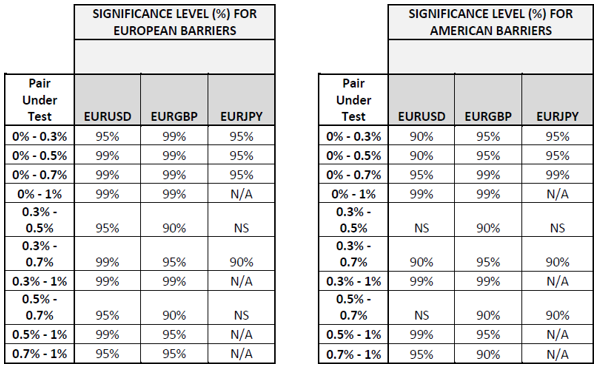
Table 7 shows the confidence levels which each combination has been found to be significant. ‘NS’ stands for ‘not significant’. As can be noted from table 7, for most cases the statistical significance was 99% and only a few were found to be statistically insignificant.

Trading Exotic option for speculative purposes

As noted earlier in this paper, the authors also tested the exotic options strategies for speculative purposes. The brokers would have the following two options:

1) Receive an upfront premium of 0.3%, 0.5%, 0.7% or 1%. One should note that the higher the built-in premium, the less attractive (and riskier) the barrier level would be.

2) Receive no premium and get the best value of the option strategy within the barrier level – the lack of upfront premium paid would be compensated with a more attractive barrier level (lower risk).

Table 8

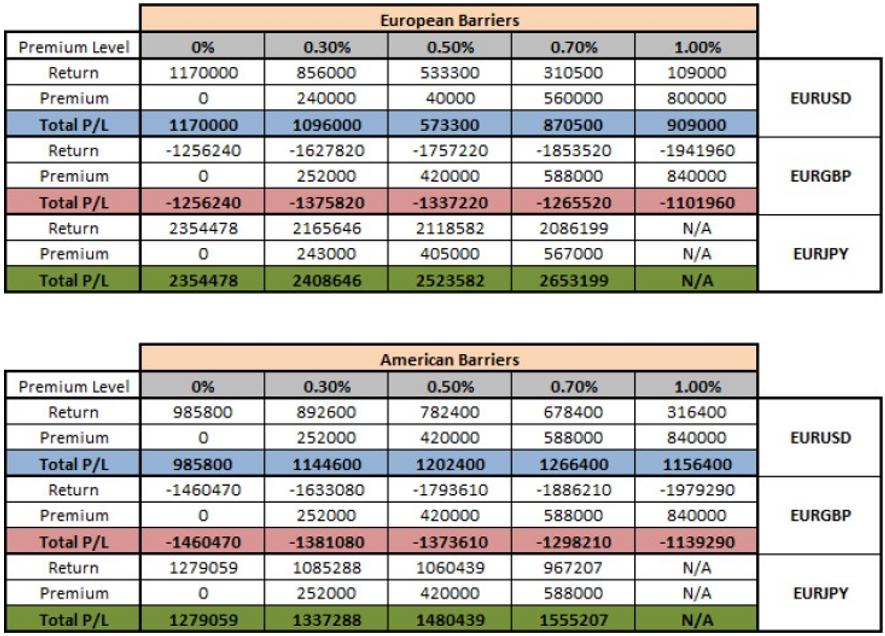
Table 8 shows the profit or loss resulting from the strategies at each built-in premium level. The total profit or loss is the return of the strategy due to market movement in addition to the upfront premium derived from the built-in premium according to the level of such premium set by the broker. For example, taking the EURUSD with a European barrier, the 0% built-in premium level derived a profit of 1,170,000 while the additional premium is zero since there was no built-in premium in this case. When one moves to the 0.3% built-in premium level, one would see the return due to market movement was less than the 0% level which stands at 856,000. However, the broker would need to add 240,000 as upfront premium from the trade which results in a total of 1,096,000. The total is still less than that from the 0% built-in premium level. The same procedure needs to be followed for all built-in premium levels.

When interpreting the above results one would find that when using the European barriers, results for EURUSD clearly shows that an increase in risk did not pay off. However, when looking into EURGBP and EURJPY results show that an increase in built-in premium amounted into a better profit or into a lower loss. The same apply for all cases when using the american barriers. Hence, one may conclude that on average brokers are better off taking higher risk and receiving an upfront premium when this is done for speculative purposes.

Summary of Findings

When considering an expiry-by-expiry, in most cases (over 97%) there is no effect on the outcome of the exotic option strategy due to an increase in built-in premium. However, when looking into the total effect of the analysis, that is, the effect throughout the whole sample of the seven year period, such effect was found to be statistically significant. Hence, this means that those 3% of cases that there was an effect on the outcome of the strategy were enough to result in a statistically significant total effect. This conclusion applies to most combinations being tested as can be seen in Table 7. There were only 5 combinations that resulted to be insignificant, two were found using the european barriers and three using the american barriers.

When testing the strategies for speculative purposes, the authors found that with the exception of the EURUSD using the european barriers, it paid off to take risk and receive an upfront premium rather than taking lower risk and relying to market movements.

Through this paper the authors conclude that the client is better off with a lower built-in premium, however, they also note that a fair amount of built-in premium is required for the industry to exist and for the brokers and market makers to make a reasonable profit to cover their costs, risks and investments.

However, the authors feel that their analysis may be the ‘spring board’ to start further analysis on the subject which may help in shedding light on the need to use such strategies. This since as far as the authors are aware there seems to be a limited number of publications tackling this subject area, even though such a market is growing year-on-year. Moreover, although, the authors are aware that with such introductions further assumptions may need to be included; It would be interesting to understand what will happen if larger risks (such as through the introduction of ratios (leverage) and knock- outs) are introduced to the strategies and compare these to their findings.